2024년 11월 1일 TIL
알고리즘 중급 강의 시간으로
최대 힙(Max Heap)과 최소 힙(Min Heap)을 배웠다.

최대 힙은
루트 노드는 항상 최대값을 가지며, 부모 노드는 항상 자식 노드 보다 큰 값을 가지는 이진 탐색 트리 였다.
최소 힙은
루트 노드는 항상 최소값을 가지며, 부모 노드는 항상 자식 노드 보다 큰 값을 가지는 이진 탐색 트리 였다.
최대 힙이라 가정하고 새로운 자식이 추가 될 경우 추가된 자식이 부모 보다
큰 수를 가질 수 있기 때문에 아래와 같은 동작 과정을 거친다.


위와 같이 동작 하기 위해 JavaScript로 구현된 코드를 보면 아래와 같이 코드가 구성 되는데,
로 MaxHeap을 Class로 구현해 생성자가 호출되면 숫자가 저장될 배열을 생성해줍니다.
만약, MaxHeap 객체에 숫자가 들어올 경우 배열의 맨 뒤(BST 트리의 맨 뒤 가지에)에 숫자를 추가해주고,
상위 부모들과 새로운 숫자를 비교하며 자리를 교체해줍다.
만약, 위와 같이 숫자가 최대 힙에 들어올 경우
힙 배열에 아무 숫자도 없기 때문에 index가 0인 위치에 10을 추가해줍니다.

배열 결과 : [10]
만약, 새로운 숫자 20이 들어올 경우 힙 배열에 [10]이 존재하기 때문에 index가 1인 위치에 20을 추가해주고,

20과 부모인 10을 비교해줍니다. 이때, 20 > 10 보다 크기 때문에

20과 10의 위치를 교체해줍니다.
배열 결과 : [20, 10]
또 다시 새로운 숫자인 5가 maxHeap에 들어올 경우, 힙 배열에 [20, 10]이 존재하기 때문에
5를 index 2의 위치에 추가해줍니다. 그 후, 5의 부모(20)과 숫자를 비교하는데
5 < 20 작기 때문에 위치를 교환하지 않습니다.

배열 결과 : [20, 10, 5]
최대 힙에 30이 들어올 경우, 힙 배열에 [20, 10, 5]가 존재하기 때문에 index가 3인 위치에 30을 추가해줍니다.

그 후, 30과 부모(10)을 비교하는데 30 > 10 크기 때문에, 30과 10 위치를 교체해줍니다.

그 후, 다시 30과 부모(20)을 비교 하는데 30 > 20 크기 때문에, 30과 20 위치를 교체해줍니다.

배열 결과 : [30, 20, 5, 10]
마지막으로, maxHeap에 15가 추가 될 경우, 힙 배열에 [30, 20, 5, 10]이 존재하기 때문에
index가 4인 위치에 15를 추가해줍니다. 15의 부모(20)과 비교했을 때 15 < 20 작기 때문에 위치를 교체하지 않습니다.
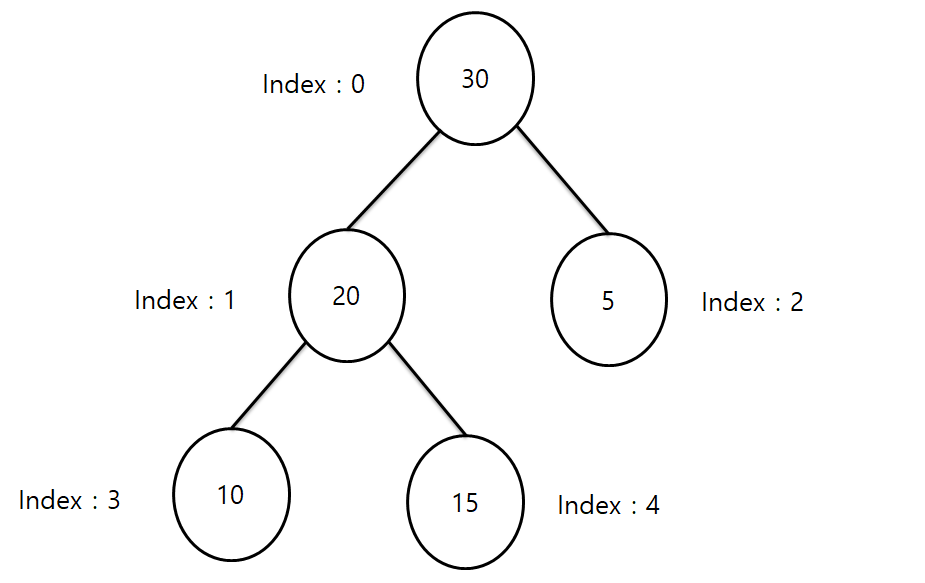
배열 결과: [30, 20, 5, 10, 15]
그 결과 MaxHeap의 힙 배열에는 [30, 20, 5, 10, 15] 순으로 숫자가 배치 돼
설명과 코드가 동일하게 동작하는 것을 확인할 수 있습니다.